NXT capabilities?
NXT capabilities?
Hello Mindboards!
I've been working on my most ambitious NXT project yet, and I've hit a (possibly very large) snag. But first, let me give some background on said project.
An NXT artillery piece. I input a compass heading and distance on an NXT in my hand, the NXT sends that via BT to the turret sitting on the floor. The turret does some trajectory calculations, then rotates and angles a zamor sphere launcher to the necessary angle, and launches a sphere, which should then land (hopefully close) on the target.
The robot is built, I've done all the trig to be able to input a compass heading and raw angle (0-45) and have the robot move to the given position.
The problem is the trajectory equation. The launcher is on the end of the turret, so when the turrets angle of elevation changes, the point the sphere is launched from changes. This causes the trajectory formula to become a differential equation; an equation that uses the value it produces inside itself, in this case, the angle. My precalc teacher is helping me figure all of that out. However, the NXT will have to do some pretty major number crunching.
So here's the big question: can the NXT handle it? Do I need special firmware to do floating point numbers and calculate trigonometric functions? If so, where can I find it? I'm planning on using NXC to program it, should I look into the BricxCC firmware?
Thanks so much! : )
I've been working on my most ambitious NXT project yet, and I've hit a (possibly very large) snag. But first, let me give some background on said project.
An NXT artillery piece. I input a compass heading and distance on an NXT in my hand, the NXT sends that via BT to the turret sitting on the floor. The turret does some trajectory calculations, then rotates and angles a zamor sphere launcher to the necessary angle, and launches a sphere, which should then land (hopefully close) on the target.
The robot is built, I've done all the trig to be able to input a compass heading and raw angle (0-45) and have the robot move to the given position.
The problem is the trajectory equation. The launcher is on the end of the turret, so when the turrets angle of elevation changes, the point the sphere is launched from changes. This causes the trajectory formula to become a differential equation; an equation that uses the value it produces inside itself, in this case, the angle. My precalc teacher is helping me figure all of that out. However, the NXT will have to do some pretty major number crunching.
So here's the big question: can the NXT handle it? Do I need special firmware to do floating point numbers and calculate trigonometric functions? If so, where can I find it? I'm planning on using NXC to program it, should I look into the BricxCC firmware?
Thanks so much! : )
-
mattallen37
- Posts: 1818
- Joined: 02 Oct 2010, 02:19
- Location: Michigan USA
- Contact:
Re: NXT capabilities?
The NXT can do just about any calculation, but it takes longer than if it was running without a byte-code interpreter. I have no idea how much math you need it to do, but the more it is, the longer it will take.
Any NXT 2.0 FW can do floating point math, and that certainly includes the latest version of EFW (the FW that comes with BCC). After installing BCC, I recommend installing the latest test release over it.
Any NXT 2.0 FW can do floating point math, and that certainly includes the latest version of EFW (the FW that comes with BCC). After installing BCC, I recommend installing the latest test release over it.
Matt
http://mattallen37.wordpress.com/
I'm all for gun control... that's why I use both hands when shooting
http://mattallen37.wordpress.com/
I'm all for gun control... that's why I use both hands when shooting
Re: NXT capabilities?
hi,
the formula for external ballistics is comparatively simple - by the NXT able to be calculated for probably a tiny fraction of a second.
These are the chart and the formula:

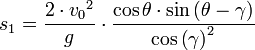
the most important but unknown variable is the deceleration behavior of the bullet due to air resistance (aerodynamic properties of different bullet shapes) which will needed to be approximated , e.g., by look-up tables established by trial-and error. The you will have to determine quite exactly the initial speed of the bullet.
Because of those bullet properties which don't go into to the mathematical equation and the difficulty to accurately determine the initial speed of the bullet it might be better to use look-up-tables for distance vs. shooting angle from the start, e.g. like those in this article:
http://www.vsms.org/Forum/Seite_26/26_0 ... hannen.pdf

the formula for external ballistics is comparatively simple - by the NXT able to be calculated for probably a tiny fraction of a second.
These are the chart and the formula:

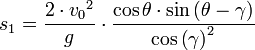
the most important but unknown variable is the deceleration behavior of the bullet due to air resistance (aerodynamic properties of different bullet shapes) which will needed to be approximated , e.g., by look-up tables established by trial-and error. The you will have to determine quite exactly the initial speed of the bullet.
Because of those bullet properties which don't go into to the mathematical equation and the difficulty to accurately determine the initial speed of the bullet it might be better to use look-up-tables for distance vs. shooting angle from the start, e.g. like those in this article:
http://www.vsms.org/Forum/Seite_26/26_0 ... hannen.pdf
Re: NXT capabilities?
Thanks for the fast replies!
I'll install the latest version of Bricxcc and the test release of the FW once I have access to a new computer (our motherboard died).
I found this formula for trajectory, it's exactly what I need: http://en.wikipedia.org/wiki/Trajectory_of_a_projectile (scroll down to how to find the angle necessary to hit (x,y))
The problem lies in the fact that to find the relative x and y coordinates of the target, the x and y coordinates of the launch point must also be known, and to find those, you must know the angle. It's a viscious circle of hard math.
The formulas for the X and Y to plug into the trajectory equation:
X=x-sqrt(496.25)*cos(theta+atan(7/44))+4
Y=y-sqrt(496.25)*sin(theta+atan(7/44))+13
where x and y (case sensitive) are the coordinates of the target, and theta is the angle of launcher elevation.
Also, how would you add an air resistance constant? Would you just multiply all the v's in the trajectory formula by the constant?
I'll install the latest version of Bricxcc and the test release of the FW once I have access to a new computer (our motherboard died).
I found this formula for trajectory, it's exactly what I need: http://en.wikipedia.org/wiki/Trajectory_of_a_projectile (scroll down to how to find the angle necessary to hit (x,y))
The problem lies in the fact that to find the relative x and y coordinates of the target, the x and y coordinates of the launch point must also be known, and to find those, you must know the angle. It's a viscious circle of hard math.
The formulas for the X and Y to plug into the trajectory equation:
X=x-sqrt(496.25)*cos(theta+atan(7/44))+4
Y=y-sqrt(496.25)*sin(theta+atan(7/44))+13
where x and y (case sensitive) are the coordinates of the target, and theta is the angle of launcher elevation.
Also, how would you add an air resistance constant? Would you just multiply all the v's in the trajectory formula by the constant?
Re: NXT capabilities?
hi,
as I already wrote,
1) the NXT is fast enough to do all the math of your formulas you want.
2) for any other requirements, you will need to have look-up-tables made by your own. Also for those, the NXT is still fast enough.
Especially the factor to calculate air resistance effects is hard to to insert into the formula and is better approached by a look-up-table.
as I already wrote,
1) the NXT is fast enough to do all the math of your formulas you want.
2) for any other requirements, you will need to have look-up-tables made by your own. Also for those, the NXT is still fast enough.
Especially the factor to calculate air resistance effects is hard to to insert into the formula and is better approached by a look-up-table.

Re: NXT capabilities?
So then it sounds like I should just do a load of test fires at different angles, plug them into my calculator, find the regression equation, then use that in the program? Figure out the math based on a table of tests?
Re: NXT capabilities?
yes, maybe - but I personally also would drop even the regression equation.
Why use a non-linear approximative equation if all and everything is based on a simple empiric table?
No equation can be as exact as (or even more exact than) your empiric table.
You can lift the canon probaly just in 1° steps (CMIIW).
so I would make a table of 90 entries of 1° each and relate it to the shooting distance.
Or make it in 30 steps of 3° each and later calculate by interpolation.
The error of your ballistic targeting accuracy (mean variation) will probably be always bigger than the accuracy error of your table...
(ps: notice that the function
angle -> distance
is not bijective!)
Why use a non-linear approximative equation if all and everything is based on a simple empiric table?
No equation can be as exact as (or even more exact than) your empiric table.
You can lift the canon probaly just in 1° steps (CMIIW).
so I would make a table of 90 entries of 1° each and relate it to the shooting distance.
Or make it in 30 steps of 3° each and later calculate by interpolation.
The error of your ballistic targeting accuracy (mean variation) will probably be always bigger than the accuracy error of your table...
(ps: notice that the function
angle -> distance
is not bijective!)
Re: NXT capabilities?
Oooh how true... 
I'll only need 45 degrees of tests, it can't move any higher.
In this case, should I use an array to store the table? I've never used arrays before, but it seems to be the right method for this situation...
I'll only need 45 degrees of tests, it can't move any higher.
In this case, should I use an array to store the table? I've never used arrays before, but it seems to be the right method for this situation...
Re: NXT capabilities?
Well after doing a number of test shots at 4 angles, I can see that that really is the best course of action. There's already a lot of slop, so an array with a table looks like for sure the best plan of action. I may make my own equation by using all the messy data points on the graph as a guide, but only because I want to be able to plug in any distance, rather than having to stick to set values on the graph. If school doesn't get in the way, this could be done in a week! 
Thanks for the help!
Thanks for the help!
Who is online
Users browsing this forum: Semrush [Bot] and 6 guests